
The detail within a fractal is incredible. What can be described in only a few lines of mathematical formulae can contain a far greater variety of forms and far more intricate detail than any artist could paint on a canvas. I find that incredible.
The most well known property of a fractal is that you can zoom in on it forever and it will always appear just as detailed. If you zoom in on anything else far enough it will not be very interesting at all. This makes fractals utterly unique, nothing else has an infinite amount of detail within it. Interestingly enough, this also means that fractals have an infinitely long perimeter, if you tried to trace it all the way around, you would never even move from where you started!
Examples of Fractals
Koch Snowflake
The snowflake is a fairly simple fractal. To build one, we start with an equilateral triangle. We split each side into thirds and replace the middle third of each side with another smaller equilateral triangle. We then repeat this process infinitely with all the new sides.
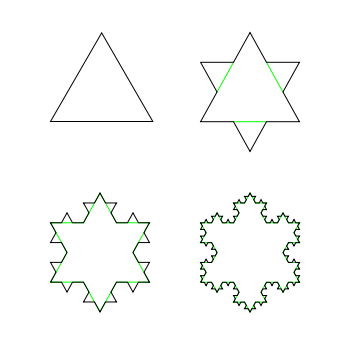
It is very simple to show that this shape has an infinite perimeter, at each step we increase the perimeter by a third. The perimeter actually grows exponentially! After repeating infinitely we will clearly have an infinite perimeter.
However, if you inscribe the original triangle within a circle, the snowflake will never cross over the circle. We have contained an infinitely long line within a finite area!
Sierpinski Triangle
I expect you have all seen this fractal before. Aside from being associated with the illuminati and Legend Of Zelda, it is also useful to explain the fractional dimensionality of fractals, after which they are named.
Again, we must start with an equilateral triangle which has a point facing upwards. We will now cut out another equilateral triangle, this one with its point facing down, so that it touches all three edges of the larger triangle. This leaves us with several triangles remaining, we will repeat this process with each smaller triangle to infinity.

As we always remove a quarter of the shape at each step, its area decreases exponentially, so when we finish, the area of the fractal is actually zero! We have cut away all of it!
As it has no area, we cannot sat it is truly 2D, but the nature of the line means it cannot be 1D either. It actually exists in about 1.6 dimensions. Click here for more information on fractal dimensionality.
The Mandelbrot Set
This is what everyone thinks of when we talk about fractals. It has evoked more wonder and mystery than any other mathematical shape.

Unlike the other fractals I have mentioned, it is not built by an iterative geometrical process, but it is actually a set of complex numbers, if we pick a colour for numbers in the set and a different colour for numbers not in the set and then colour the complex plane based on whether each number is in the set or not, we will get the famous fractal shape.
A complex number c is in the mandelbrot set if the following series stays small, if it approaches infinity then c is not in the set.
Zn+1 = Zn2 + c; Z0 = 0
Even if you do not understand complex numbers, I think the fact that such a simple mathematical equation can generate such beauty and wonder incredible. Unlike the previous fractals, the mandelbrot set has a huge variety of forms within it, a few of which I show below, along with their often amusing nicknames.
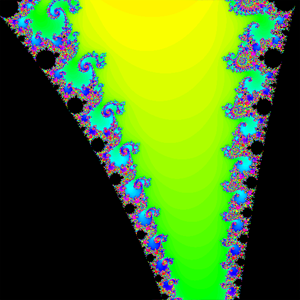 Seahorse Valley |
 Elephant Valley |
Fractals in Nature
Fractals are not a purely mathematical construct. While true infinite detail is impossible to reach in reality, fractal-like shapes are incredibly common in the natural world, particularly in biology.
Whenever an incredibly large surface area is needed, such as when transferring air from our lungs to our blood or for a gecko trying to grip onto vertical surfaces, fractals are the perfect solution - being able to have incredibly vast surface areas within only a small amount of space.
The weather is another example. From huge clouds and airflows working their way around the globe to the steam swirling out of a cup of tea and the flap of a butterflies wings, the weather system is interesting and detailed.
An example of where fractals have proved incredibly useful is in measuring coastlines, or rather not measuring coastlines. As coastlines follow a fractal shape, the more accurately you measure them, the longer they appear to be with no limit on this length - as they are fractal like, their true length is near infinite after all. This makes any measurement of the length of a coastline fairly meaningless.
We should, however, give sailors the respect they deserve - how on earth do they ever find port when it is just a small part of an infinitely long line?






